🡐 BACK TO RESOURCES
Singapore Math Heuristics: Draw a Table, Make Suppositions and Use Before-After Concept

Heuristics, in the context of problem-solving, are a set of strategies to help students solve mathematical problems.

Although problem-solving is by and large the process of working towards a goal to which a solution may not be immediately present, it is important that problem solvers (or students) are not only aware of what they are doing and why they are doing it, but also have the ability to self-regulate these processes.

This is where the role of metacognition in problem-solving comes in. Metacognition is the awareness of how your mind works and the ability to control your thinking process.

When students understand and recognise how they learn and are given opportunities to monitor and regulate their thinking during problem-solving, not only do they improve their metacognitive skills but they may also be more successful in solving the problem.

Singapore Math Heuristics

In part one of our Math Heuristics series, we gave an overview of the 12 heuristics in Singapore Primary Math syllabus, with tips from the curriculum team at Seriously Addictive Mathematics (S.A.M) on how to solve various math word problems using them.

In part two of the Math Heuristics series, we expanded on the heursitics – Act It Out, Draw A Diagram and Look For Patterns, and also demonstrated how to apply the Polya’s 4-step problem-solving process in sample word problems.

In part three of the Math Heuristics series, we focused on the heuristics: Make a Systematic List, Guess and Check, and Restate the Problem in Another Way.

In part four of the Math Heuristics series, we looked at three heuristics: Solve Part of the Problem, Simplify the Problem and Work Backwards.

In the final part of the series, we will explore the remaining heuristics: Draw a Table, Make Suppositions and Use Before-After Concept.

_______________________________________________________________________________________________________

Heuristic: Draw a Table

Word Problem (Grade 4):

Mary cycles to the park every 6 days. John cycles to the same park every 8 days. Mary and John cycle to the park on 3 June, Tuesday. On which date and day will they cycle to the park together on the same day?

Solution:

1. Understand:
What to find: date and day Mary and John next cycle to the park on the same day.
What is known: Mary cycles to the park every 6 days. John cycles to the park every 8 days. Mary and John cycle to the park on 3 June, Tuesday.

2. Choose: Draw a table

3. Solve:
Let’s compare the days Mary and John cycle to the park.
Mary cycle to the park on days in multiples of 6.
John cycle to the park on days in multiples of 8.

Mary and John will cycle to the park on the same day every 24 days.
3 June + 24 days is 27 June
24 days = 3 weeks and 3 days
Tuesday + 3 days is FridayMary and John will next cycle to the park on 27 June, Friday.4. Check
Is 24 a multiple of 6? Yes
Is 24 a multiple of 8? Yes
Is 27 June Friday 24 days after 3 Jun Tuesday? Yes

Try solving the following word problem using Polya’s 4-step process.

Word Problem (Grade 4):

Janice wanted to distribute stickers equally among some children. If each child received 8 stickers, she would have 3 stickers left. If each child received 11 stickers, she would need another 9 stickers. How many children were there?
Answer: Janice had 35 stickers. There were 4 children.
See the solution in part one of our Singapore Math Heuristics series.

_______________________________________________________________________________________________________

Heuristic: Make Suppositions

Word Problem (Grade 5):

Mary took a Science test. She answered all 30 questions and obtained 42 marks. For each correct answer, 3 marks were awarded. For each wrong answer, 1 mark was deducted. How many questions did she answer correctly?

Solution:

1. Understand:
What to find: Number of questions Mary answered correctly.
What is known: Mary answered 30 questions. She obtained 42 marks. 3 marks were awarded for each correct answer. 1 mark was deducted for each wrong answer.

2. Choose: Make suppositions

3. Solve:
Suppose that Mary answered all 30 questions correctly.
30 x 3 = 90
Mary obtained 92 supposed total marks.

90 – 42 = 48
The supposed total marks are 48 more than the actual total marks.

3 + 1 = 4
By replacing 1 correct answer with 1 wrong answer, 4 marks are deducted from the total marks.

48 ÷ 4 = 12
Mary answered 12 questions wrongly.

30 – 12 = 18
She answered 18 questions correctly.

4. Check:
What are the total marks awarded for 18 correct answers?
18 x 3 = 54
What are the total marks deducted for 12 wrong answers?
12 x 1 = 12
What are the total marks obtained by Mary?
54 – 12 = 42

Try solving the following word problem using Polya’s 4-step process.

Word Problem (Grade 4):

Farmer James has some ducks, horses and cows on his farm. He has 30 ducks and cows altogether. The total number of legs the ducks and cows have is 82. The total number of legs the horses have is 28. How many ducks and how many cows are there on the farm?

Answer: There are 19 ducks and 11 cows on the farm.
See the solution in part one of our Singapore Math Heuristics series.

_______________________________________________________________________________________________________

Heuristic: Use Before-After Concept

Word Problem (Grade 5):

The ratio of Joy’s age to her uncle’s age is 1 : 4 now. In 21 years’ time, the ratio of Joy’s age to her uncle’s age will be 3 : 5. How old is Joy’s uncle now?

Solution:

1. Understand:
What to find: Joy’s uncle age now.
What is known: The ratio of age now is 1 : 4. The ratio of age 21 years later is 3 : 5.

2. Choose: Use before-after concept

3. Solve:

(9 – 2) units = 7 units = 21 years
1 unit = 21 ÷ 7 = 3 years
8 units = 3 x 8 = 24
Joy’s uncle is 24 years old now.4. Check:
How old is Joy now? 3 x 2 = 6 years old
Ratio of Joy’s age to her uncle’s age now = 6 : 24 = 1 : 4
How old is Joy 21 years later? 3 x 9 = 27 years old
How old is Joy’s uncle 21 years later? 3 x 15 = 45
Ratio of Joy’s age to her uncle’s age 21 years later = 27 : 45 = 3 : 5

Try solving the following word problem using Polya’s 4-step process.

Word Problem (Grade 5):

Ray and Sam each brought some money for shopping. The ratio of the amount of Ray’s money to the amount of Sam’s money was 3 : 4. After each of them bought a laptop for $1250, the ratio of the amount of Ray’s money to the amount of Sam’s money became 1 : 3. How much money did Sam bring for shopping?
Answer: Sam bought $2000 for shopping.
See the solution in part one of our Singapore Math Heuristics series.

This is the final part to S.A.M Math Heuristics series. Read part one, part two, part three and part four here.

Established in 2010, Seriously Addictive Mathematics (S.A.M) is the world’s largest Singapore Math enrichment program for children aged four to 12. The award-winning S.A.M program is based on the global top-ranking Singapore Math curriculum with a focus on developing problem solving and thinking skills.

The curriculum is complemented with S.A.M’s two-pillared approach of Classroom Engagement and Worksheet Reinforcement, with an individual learning plan tailored to each child at their own skill level and pace, because no two children learn alike.

← BACK TO RESOURCES
MORE ARTICLES

Singapore Math Heuristics: Solve Part of the Problem, Simplify the Problem and Work Backwards

Problem-solving in mathematics helps children develop reasoning and communication skills that are transferrable and important life skills. Reasoning is required on three levels when children solve word problems. First, they use reasoning to recognise what information is provided or missing. Then, they use reasoning to figure out what information they need to find. Finally, they […]

READ MORE🡒

Singapore Math Heuristics: Make A Systematic List, Guess And Check, Restate The Problem In Another Way

The skills children pick up in math are indispensable; they can be applied to other academic subjects and to solve real-world problems in their daily lives and future work. The Singapore Math curriculum focuses on problem solving. Through problem solving, children develop thinking skills such as creative thinking and critical thinking. When children analyse math […]

READ MORE🡒

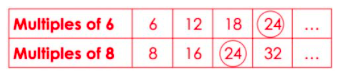
Singapore Math Heuristics: Act It Out, Draw A Diagram, Look For Patterns

In part one of our Singapore Math Heuristics series, we gave an overview of the 12 heuristics in Singapore Primary Math syllabus, with tips from the curriculum team at Seriously Addictive Mathematics (S.A.M) on how to solve various math word problems using them. To recap, heuristics are methods or strategies students can use to solve complex […]

READ MORE🡒

What are Singapore Math Heuristics?

Ever tried to help your child with primary math homework and got stumped? Today’s math questions can be challenging – even for adults. Math education is changing. While many parents spent time memorising procedures and formulas, today’s students are expected to not only understand and master the concepts, but also to have strong thinking skills […]

READ MORE🡒