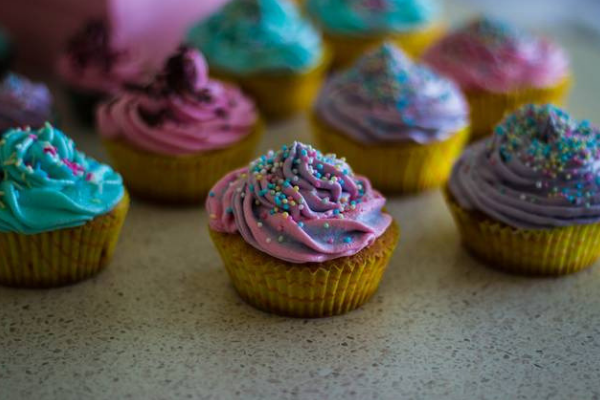Singapore Math Heuristics: Solve Part of the Problem, Simplify the Problem and Work Backwards
Problem-solving in mathematics helps children develop reasoning and communication skills that are transferrable and important life skills.
Reasoning is required on three levels when children solve word problems. First, they use reasoning to recognise what information is provided or missing. Then, they use reasoning to figure out what information they need to find. Finally, they use reasoning to draw on relevant prior knowledge and choose the most suitable heuristic to work out the solution.
Communication is required for comprehension and expression during problem-solving. Children need to read and understand word problems and then write and express their solutions. When children are encouraged to explain their thinking verbally, visually and in written form, they gain a better understanding of math concepts and develop stronger communication skills.
Singapore Math Heuristics
In part one of our Math Heuristics series, we gave an overview of the 12 heuristics in Singapore Primary Math syllabus, with tips from the curriculum team at Seriously Addictive Mathematics (S.A.M) on how to solve various math word problems using them.
In part two of the Math Heuristics series, we expanded on the heursitics – Act It Out, Draw A Diagram and Look For Patterns, and also demonstrated how to apply the Polya’s 4-step problem-solving process in sample word problems.
In part three of the Math Heuristics series, we focused on the heuristics: Make a Systematic List, Guess and Check, and Restate the Problem in Another Way.
In part 4 of this series, we will zoom in on these 3 heuristics: Solve part of the problem, simplify the problem and work backwards.
_______________________________________________________________________________________________________
Heuristic: Solve part of the problem
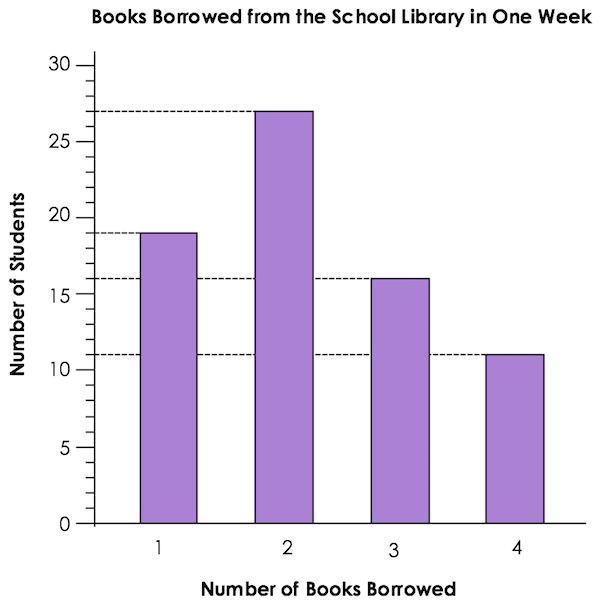
Word Problem (Grade 3):
At a school library, each student could borrow up to 4 books. The bar graph below shows how many books students borrowed from the school library in one week. What was the total number of books borrowed from the library that week?
_______________________________________________________________________________________________________
Heuristic: Simplify the problem
Word Problem (Grade 3):
A bakery sold cupcakes at $4 each. For every 6 cupcakes bought, a discount of $2 was given. Ling bought 50 cupcakes. How much did Ling pay for the cupcakes?
Word Problem (Grade 4):
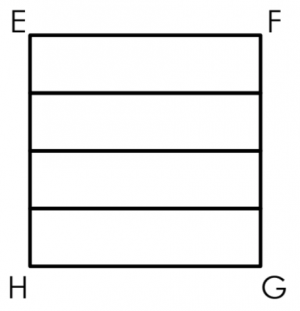
Square EFGH is made up of 4 rectangles. The perimeter of Square EFGH is 32 centimetres. Find the perimeter of each rectangle.
Try solving the following word problem using Polya’s 4-step process.
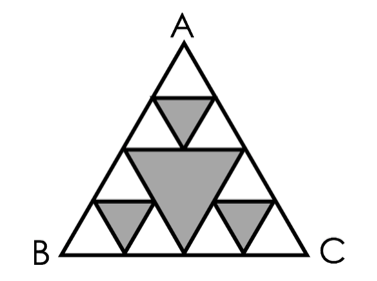
Word Problem (Grade 6):
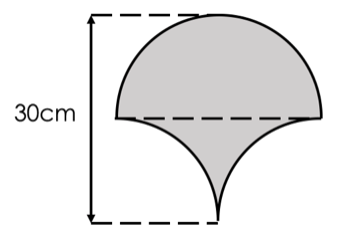
The shaded figure below shows a semicircle and two quarter circles. Find the area of the shaded figure. (Take pi = 3.14)
_______________________________________________________________________________________________________
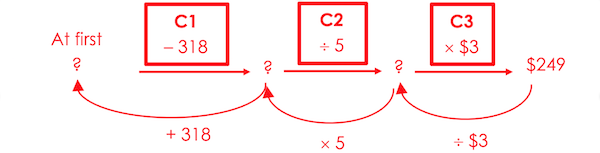
Heuristic: Work backwards
Word Problem (Grade 3):
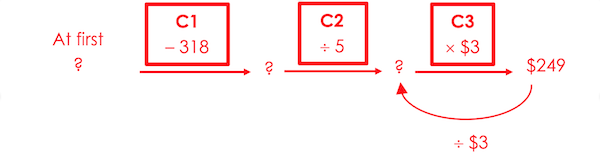
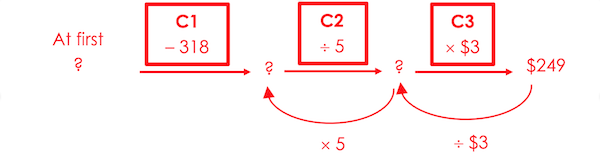
Mr Adam had some pens in his stationery store. He sold 318 of the pens at $1 each. He then put the remaining pens into packs of 5 and sold each pack for $3. He made $249 from selling all the packs. How many pens did Mr Adam have at first?
Try solving the following word problem using Polya’s 4-step process.
Word Problem (Grade 3):
Darren had some stickers in his collection. He bought 20 more stickers and gave 33 stickers to his sister. He had 46 stickers left. How many stickers did Darren have in his collection at first?
Look out for the final part of this series for the remaining Math Heuristics and word problems with step-by-step worked solutions.
This is the fourth part to S.A.M Math Heuristics series. Read part one, part two and part three here.
Established in 2010, Seriously Addictive Mathematics (S.A.M) is the world’s largest Singapore Math enrichment program for children aged four to 12. The award-winning S.A.M program is based on the global top-ranking Singapore Math curriculum with a focus on developing problem solving and thinking skills.
The curriculum is complemented with S.A.M’s two-pillared approach of Classroom Engagement and Worksheet Reinforcement, with an individual learning plan tailored to each child at their own skill level and pace, because no two children learn alike.